 top
top top
top| A feel for big numbers, with grains of salt |
|
| salt grains |
|
Counting...
(with a grain of salt, say ±50%)
| a grain of salt | One | 100 | 1. |
| some grains | ten | 101 | 10. |
| a tiny pile | hundred | 102 | 100. |
| a pinch | thousand | 103 | 1,000. |
| 1/4 teaspoon | ten thousand | 104 | 10,000. |
| tablespoon | hundred thousand | 105 | 100,000. |
| 1/2 cup | million | 106 | 1,000,000. |
| ten million | 107 | 10,000,000. | |
| hundred million | 108 | 100,000,000. | |
| a bathtub | billion | 109 | 1,000,000,000. |
| ten billion | 1010 | 10,000,000,000. | |
| hundred billion | 1011 | 100,000,000,000. | |
| a classroom | trillion | 1012 | 1,000,000,000,000. |
Perhaps this would be better done with sugar, as it tastes better...
With a 1mm grain size, it would be something like:
| sugar grains |
|
With 1/4 billion people (1/4 bathtub of grains) in
the US... How much are under 14 years old? Unemployed? How fast
is salt being added by birth? Removed by death?
(Lots of
stats available...)
With a room filled to the ceiling with a trillion grains, when you
open the door and paw at it with cupped hands, how much/fast do you
move? With a shovel? A bucket?
(The US
budget is a trillion and a half dollars. How much per day?
Second? How much is Medicare? Social security? Education? Space?)
Salt is fascinating stuff. Roman legions were payed in it, cities taxed, evaporating salt-water for it was a crime. Politics, rebellions, required for life, preservation of food. Perhaps someone has done a web page...
Comments encouraged. - Mitchell N Charity <mcharity@lcs.mit.edu> |
History: 2003-Feb-03 Fixed 2 links. 2000-Oct-17 Repointed "stats" link to something similar that works. Thanks to a reader. 1997.May Created.
Some details about this page:
The back of my envelope...
I'm using "Morton Salt" (table salt).
First, some quick and dirty work...
The grains measure about 1/2 mm,
which gives 20/cm 8000/cm3 8 x 109/m3 1010/m3
Its box is a cylinder 6 x 10-4 m3 (8cm d, 12cm h),
and masses 0.737 kg,
so thats a density of about 1.2 kg/m3 (1.2 g/cm3).
So 10-10 kg/grain, and 5 x 106 grains in the box.
More carefully measuring the grains,
I get 0.5 +- 0.05 (about 1 grain uncertainty in 5mm).
Upping the sample to 10mm didnt seem to help narrow the uncertainty
(due to grain size variations).
With this big an uncertainty, I'm not going to worry about how
tighly packed the grains are.
thus
20/cm (+-2) 6000 to 11000 /cm3 0.6 to 1.1 × 1010
so 1010 (+10%-40% for measurement uncertainty)
which gives worst-case percent errors of +70% and -10%.
So, probably an overestimate, possibly by a factor of 2, but not
much of an underestimate.
So...
grains/m3 1010 × 0.6 to 1.1
kg/grain 10-10 × 1 to 2
grains/kg 1010 × 0.5 to 1
Ok, what are some accessible volumes.
teaspoon 4.9x10-6 m3
tablespoon 1.5x10-5 m3
cup 2.4x10-4 m3
gallonUS liquid 3.8x10-3 m3
foot3 0.028 m3
bathtub ~0.2 m3 (~8 ft3)
classroom ~200 m3 (10x8x2.5 m)
So
teaspoon 3 to 6 × 104, or
tablespoon 0.9 to 2 × 105
cup 1 to 3 × 106
bathtub 1 to 2 × 109
classroom 1 to 2 × 1012
Ok. Time for a reality check.
A big pinch looks about 103 grains
(by dividing it in half a couple of times and then counting).
So a 1/4 teaspoon seems 104 or two.
Which sortof fits.
(_This_ time it fits. The first time it didn't.
Turned out I had mangled the object vs # grains paragraph.
And in tracing it down, I would have done a lot better to
let the numbers lead me, rather than having an emotional stake
in their fitting. A lesson.)
I could do this more carefully, but for now...
Call it
a 1/4 teaspoon for 104
a tablespoon for 105
a 1/2 cup for 108
a bathub for 109
a classroom for 1012.
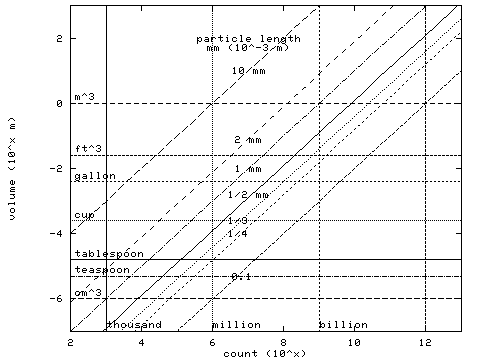
I should address the non-linear error "feel". 50% seems a bigger deal for big numbers than for small ones.