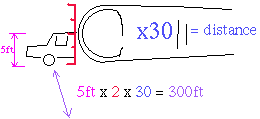Measuring Angle and Distance with your Thumb

(Now part of A View from the Back of the Envelope.)

The idea: By holding out your thumb to measure angles, you can tell your distance to things (people, cars, buildings, planes, clouds, etc).

This is a Body Ruler page.

Quick examples

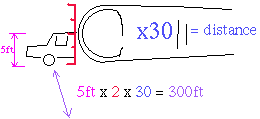
I hold out my arm, look at my thumb, and see a distant car half as high. Cars are about 5 feet (1.5 meters) high. So my thumb appears 10 feet (3 meters) wide. And since I know (see below) my thumb is x30 times as far as it seems tall... I know the car is something like 300 feet (90 meters) away!

Huh?

Hold your arm straight out in front of you. Make a fist. Point it at a window. The window will appear a couple of fists high. The further away the window, the fewer the fists. Windows in nearby buildings won't even be a fist tall, they will perhaps be a couple of thumb-widths high. Or less. Stick your thumb out sideways. Point your arm at a nearby building. Count how many thumbs high its windows are.

Ok, but how do you tell how far away it is? You need to know two things:
very roughly how big windows are (I don't know, say something like 5 feet),
and that your thumb covers things 30 times bigger.

So, a 5 foot window, which seems 2 thumbs high, makes your thumb look 3 feet wide (5 feet / 2 thumbs), and thus something like 90 feet (3 x 30) away.

Thumbs and Fists and ROUGH Distance

In general, people's thumbs and fists are about:

size	distance is	(angle)
fist	x 6	10°
thumb	x 30	2°
½ thumb	x 60	1°
¼ thumb	x 120	½°

Or you can just remember that your thumb is x30, and each time you halve your thumb, its twice as big.

Examples

Cars are about 4 meters (12 feet) long.
A parked car across the street which is about 3 thumb-widths long is... 40 meters (120 feet) long. (12 / 3 x 30)
Cars are about 1.5 meters (5 feet) high.
The same parked car is about 1 thumb high, so... 45 meters (150 feet). (1.5 m (or 5 ft) x 30)
Notice this is only roughly the same as the previous estimate.
How roughly is discussed in the next section.
Cars are about 2 meters (6 feet) wide.
So the car, ahead of you on the road, which is 1/2 thumb wide, is roughly 120 meters (360 feet) away.
People are about 1-2 meters (3-6 feet) tall (kids/adults).
Office building floors are about 4 meters (10 feet) high.
So if a 30 story building is 6° (two fingers) high, then its about 30 x 4 (or 10) x 20 = 2400 meters (6000 feet)... so something like a mile away.
Airline jets are about 40 meters (150 feet) long. source[link broken]
So a jet flying by and 1/4 thumb wide is about 150 x 120 = 18000 feet away (3+ miles).
If its say 3 fists up (30°) [described below], then its 1/2 x 18000 = at about 9000 feet altitude, and about the the same 3'ish miles away on the ground.
How far away is that cloud?
Clouds can come at different altitudes, so you need to find out the current cloud ceiling (how high the bottom of the clouds are). If the clouds are at 1500 feet, and the cloud you are interested in is say one fist up from the ground, then its approx 10 x 1500 = 15000 feet (3ish miles) away.
How to find out cloud ceilings?
Well, if anyone knows an easy to use web resource, I'd like to know it.
There are a couple of interfaces to the METAR data, but not all of them decode the ceiling information, and they seem a bit experimental/unstable (as of 1997.Mar.25). I expect things will improve. I found:

Really?

How "roughly, approximately, something like, about" is this?
You will often be within a factor of 2 or 3, and by using greater care, can get it under 20%.

Sources of error:

Measuring the angle. Error in the angle measured shows up linearly as error in the distance estimate. So if your angle measurement is off by 30%, so will your distance estimate be. And similarly, if you mismeasure something as 1 thumb rather than 2, or as 1/2 rather than as 1/4, you'll add a factor of 2 error. The smaller the angle, the harder it is to get close. Sources of error are:
- Did a quick and dirty measurement. To improve, take some time and do a more careful one.
- Angle too small to be convenient. Like 1/10 of a thumb. To improve, find something else to measure with. Like the thickness of a key, or a pencil lead, or ... See calibration below.
- Calibration error. If your thumb is really 10% narrower than our imaginary 2° thumb, then your distance estimates with be 10% high. To improve, fudge in a correction (ie, nudge your distance estimates up or down to compensate), or calibrate part of your thumb more precisely. See calibration below.
- Holding your arm out. Small changes in the distance from thumb to eye don't cause much error.
- Drifting calibration. Parts of your thumb are bigger than others. Once you start trying for close calibration, you need to choose one part of your thumb and stick with it.
Estimating the object size. Error in object size shows up linearly as error in the distance estimate. So if your object size estimate is 20% high, your distance estimate will be too. If you use an object a lot, but dont have a good estimate, you might want to improve it. (Like finding out how tall a skyscraper really is, rather than estimating from the number of floors.)
Doing the math. You can simplify your math by being approximate (5 / 3 = 2 , rather than 2.5). This can add error. So if you want a closer estimate, you can avoid such simplifications. But, there is no point in trying to make your math more precise than your measurement and estimates. For instance, the 5/3=2 adds a 20% error, but if your object size estimate is only good to within a factor of 3 (ie, it could be 3 times bigger, or 1/3 smaller), the 20% is not important.
The angle multiplyer.I've said a 2° degree thumb gives you a x30 distance. Its really more like 28.7 (1/sin(2°)). The error is consistently about 5% high, which seems well worth the simplification.

angle multiplyer error (closer)

1/4° 240 5% (229)

0.5° 120 5% (114)

1° 60 5% (57.3)

2° 30 5% (28.6)

6° 10 5% (9.57)

10° 6 4% (5.76)

20° 3 3% (2.92)

Calibrating Yourself

The idea is to see how big various things are (fingers, different parts of fingers, combinations of fingers, fist, and perhaps some things you generally have with you, like keys). Then you can find some specific part of your body (like the middle of your thumb nail, or the end of one of your fingers), which is just under 2 degrees. This can then be your angle measurer.

For instance, I personally use the outermost joint of my pointer finger. Not my thumb, which is slightly too big.

There are lots of ways to set up for calibration.

The easiest is to just put things against a rule that has already been calibrated, like this chart or these cards.

Another approach is to draw some degree lines on a wall, and then step back the right distance. The key is that one stand back ~57 times the degree-line separation. Here are some example(s):

Draw lines on pieces of paper, dividing them into 4 parts ( ie, a line in the middle, and 2 in the middle of them, and maybe one on the very edge, just so you can see the edges when the papers are put together). Tape the papers to the wall in a tower, and step back 14 papers-worth of distance. (14 is 1/sin(4°). We could have done 6° per paper, but at only 10 papers distance, shifting your body confuses things.)
...

Things up in the air

When you have measured the distance to something up in the air, like an airplane, it can be nice to separate its altitude from its ground distance.

Here is one simplification, admittedly not very simple.
We should work out one with just 3 or 4 numbers to remember, as this one's 5% error is excessively precise for most stuff.

angle altitude factor
sin(angle) ground distance
cos(angle)

0° (its on the ground) 0 1

10° (1 fist up) 1/6 1

20° (2 fists up) 1/3 1

30° (3 fists up) 1/2 5/6

40° (4 fists up) 2/3 2/3

50° (5 fists up) 2/3 2/3

60° (3 fists down) 5/6 1/2

70° (2 fists down) 1 1/3

80° (1 fist down) 1 1/6

90° (up) 1 0

which hovers around 5% error.

[** ... **]

Details, details

[** ... **]

Blinking your eyes instead

A reader writes

   When I was about 13 years old (1947) I remember reading somewhere
   (maybe a Boy Scout handbook) that you could estimate distance by
   holding your thumb out in front of you and sight an object with one
   eye closed, then without moving open that eye and sight the object
   with the other eye closed; then estimate how far your thumb
   appeared to move and multiply that number by eight.

Which seems about right. Instead of defining an angle using one eye and two thumb edges, it uses two eyes and one thumb edge. The angle is a bit wider. The distance between one's eyes is about 4 thumbs wide, so 8x sounds reasonable (30x/4).

I wonder if people vary less in their eye "widths", then in their thumb widths. If so, then this approach would have less need for personal calibration.

Links

At Arm's Length a NOVA Teacher's Guide.
Up, Up, and How Far Away?

I welcome questions, comments, and thoughts. - mcharity@lcs.mit.edu.
[Top] [Musings] [Body Ruler]

Notes:
  This page hasn't drawn much comment over the years,
    and thus hasn't been pursued.

Doables:
  Cleanup.
  Try describing from an similar triangles / LvH ratio perspecive.

History:
  2003-Jul-16  Added a reader's note on blinking.  Thanks!
  2003-Feb-04  Fixed 1 link, flagged 4.  Moved WeatherNet ahead of broken services.
  2001-Aug-14  Ripped out `hold rule at arms length' approach to here.
  2001-Aug-09  Added `hold rule approach' (thanks to a reader's question
               about measuring distance for archery).
  1998.Dec.01  Added links to NOVA Balloon science pages.  (Thanks go to a reader.)
  1997.May.05  Added link to A View from the Back of the Envelope.
  1997.Mar.25  Draft fleshed out.
               I will work it further if people are interested.
  1997.Mar.24  Draft begun.
  1997.Mar.23  Idea.

angle	multiplyer	error	(closer)
1/4°	240	5%	(229)
0.5°	120	5%	(114)
1°	60	5%	(57.3)
2°	30	5%	(28.6)
6°	10	5%	(9.57)
10°	6	4%	(5.76)
20°	3	3%	(2.92)

angle	altitude factor sin(angle)	ground distance cos(angle)
0° (its on the ground)	0	1
10° (1 fist up)	1/6	1
20° (2 fists up)	1/3	1
30° (3 fists up)	1/2	5/6
40° (4 fists up)	2/3	2/3
50° (5 fists up)	2/3	2/3
60° (3 fists down)	5/6	1/2
70° (2 fists down)	1	1/3
80° (1 fist down)	1	1/6
90° (up)	1	0