Some thoughts on differential equation notation - functional vs classical
The idea
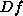 is a nice alternative to
is a nice alternative to 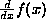
The idea: modern functional notation for derivatives
is a nice alternative to the commonly used classical notation. I find
it is easier to understand, less ambiguous, lends itself to execution,
and has less tendency to motivate little deceits.
CREDITS: Most of these ideas come from an old
draft of "Variational Mechanics: a Functional
Approach" (as yet unpublished?), by Harold Abelson, Meinhard
Mayer, Gerald Sussman, and Jack Wisdom. The idea for the extended
example below comes, via them (page vi), from Michael Spivak's
Calculus on Manifolds (1965).
[Update 2001 - The book is now available as the
Structure and Interpretation of Classical Mechanics! ]
The mistakes are my contribution.
I hope they will forgive me for lifting a particularly fun quote
(from the Preface, page v):
"In almost all textbooks, even the best, this principle is
presented so that it is impossible to understand." (K. Jacobi
Lectures on Dynamics, 1842-1843). I have not chosen to break
with tradition.
V.I. Arnold, Mathematical Methods of Classical Mechanics
(1980), footnote on p.246
Contents
A side by side look at various expressions
Some problems with the classical notation
An equation worked in both notations
Executing the functional notation (an almost empty section)
| classical: |
functional: |
meaning: |
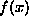 |
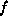 |
a function, f, of one variable |
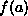 or or 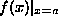 |
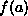 |
the value of f when it is evaluated at a |
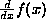 |
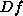 |
the derivative of f, which is itself a function!
It takes the same arguments as f does. |
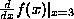 |
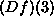 |
the value of the derivative of f, when it is evaluated at 3 |
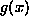 |
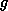 |
another function |
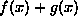 |
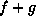 |
a function, the sum of two functions which take the same arguments |
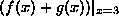 |
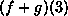 |
the value of 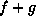 when it is evaluated at 3
(namely the sum of the values of f and g when both are evaluated at 3) when it is evaluated at 3
(namely the sum of the values of f and g when both are evaluated at 3) |
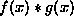 |
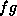 |
a function, the product of two functions which take the same arguments |
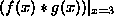 |
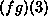 |
the value of 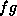 when it is evaluated at 3
(namely the product of the values of f and g when both are
evaluated at 3) when it is evaluated at 3
(namely the product of the values of f and g when both are
evaluated at 3) |
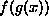 |
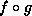 |
a function, the composition of f and g (ie,
f is called on the result of g called on the argument to
the new function). It thus takes the same arguments as g. |
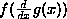 |
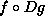 |
another function, the composition of f and the derivative
of g (ie, f is called on the result of Dg called
on the argument to the new function) |
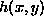 |
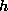 |
another function |
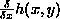 |
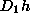 |
the partial derivative of h
with respect to its 1st argument |
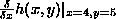 |
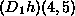 |
the value of 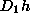 when evaluated at (4,5)
(namely, the partial derivative of h, in the neighborhood of (4,5),
with respect to its first argument) when evaluated at (4,5)
(namely, the partial derivative of h, in the neighborhood of (4,5),
with respect to its first argument) |
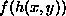 |
 |
the composition of f and h |
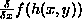 |
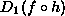 |
the partial derivative of  with respect to its 1st argument. with respect to its 1st argument.
|
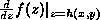 |
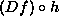 |
a function (of course), which gives the derivative of f at values given by h |
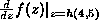 |
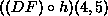 |
the derivative of f at the value of h evaluated at (4,5) |
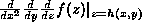 |
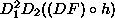 |
hmm... what do you think? |
- Obscurity creates teaching difficulties, such as the alleged need
to explain to beginning students why you can't evaluate
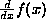 at 3 (ie (Df)(3)) by substituting 3 for x,
(producing
at 3 (ie (Df)(3)) by substituting 3 for x,
(producing 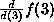 nonsense).
nonsense).
- Which is clearer? The chain rule expressed as
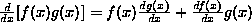 ,
,
or as
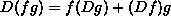 .
.
- But more fundamentally, classical cumbersomeness motivates
pathologies. A verbose equation needs to be shrunk. To shrink an
equation, content is stripped out and scattered to the surrounding
text. To gain some conciseness, ambiguity is used, with similar
expressions meaning different things in different parts of an
equation. This can then corrupt the associated reasoning (ie, there
are allegedly a number of derivations of Hamilton's equations, which
contain a step asserting "and now we consider the momentum to be
independent of the velocities", an obvious absurdity, apparently
motivated by notational opacity).
Lets dissect an classical example, and then compare the functional equivalent.
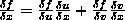
where f(u,v) is a function of u=g(x,y) and v=h(x,y).
For ambiguity, lets see what three seemingly similar subexpressions mean (
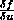 ,
, 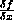 ,
, 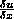 ):
):
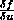 |
means the partial derivative of f with
respect to its first argument u |
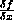 |
means 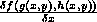 |
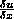 |
means 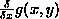 |
So can you tell what an equation expression 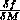 means just by looking at it? No. To disambiguate it one has to play
detective and examine the variables and the surrounding text.
means just by looking at it? No. To disambiguate it one has to play
detective and examine the variables and the surrounding text.
In contrast, here is the functional version.
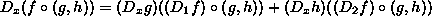
The meaning of this equation can be determined systematically from
the meaning of its parts.
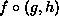 is a function. It takes the same
arguments as g and h take (thus g and h
must both be taking the same kind of arguments). f itself
takes two arguments, one from g and one from h.
The function gives the values f gives, when f is given
the values g and h give, when both given same
arguments.
Expressed differently: there are some arguments. g and
h independently chew on them. Their two results are given to
f, which then provides the final result.
is a function. It takes the same
arguments as g and h take (thus g and h
must both be taking the same kind of arguments). f itself
takes two arguments, one from g and one from h.
The function gives the values f gives, when f is given
the values g and h give, when both given same
arguments.
Expressed differently: there are some arguments. g and
h independently chew on them. Their two results are given to
f, which then provides the final result.
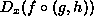 is a function. It is the derivative of
is a function. It is the derivative of
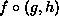 with respect to one of its arguments,
x. The function's arguments are the same as those of
with respect to one of its arguments,
x. The function's arguments are the same as those of 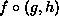 ,
, 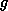 and
and 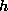 . In english, it is the rate of change in the
values f gives (f's arguments having been provided by
g and h from their arguments), in the neighborhood
specified by those same arguments, as one of those arguments
(x) varies.
. In english, it is the rate of change in the
values f gives (f's arguments having been provided by
g and h from their arguments), in the neighborhood
specified by those same arguments, as one of those arguments
(x) varies.
Perhaps expressed more clearly... g and h take
identical arguments. Those arguments define a point in space.
g and h each provide some value for that point.
f computes its own value for that point, computing it from the
values given by g and h. As one of those arguments,
x, varies, jiggling the point, the value of f also
jiggles. How fast f jiggles relative to the argument's
jiggling is the subject of this equation.
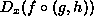 is just a way of saying this.
is just a way of saying this.
As for the right hand side...
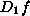 is a function. It takes the same
arguments as f does. Its the partial derivatives of f
with respect to its first argument. This is how fast f
jiggles, in general, compared to its first argument's jiggling.
is a function. It takes the same
arguments as f does. Its the partial derivatives of f
with respect to its first argument. This is how fast f
jiggles, in general, compared to its first argument's jiggling.
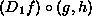 is a function. It takes the same
arguments as g and h do. Its values are the values the
function
is a function. It takes the same
arguments as g and h do. Its values are the values the
function 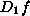 gives, when given the values that
g and h give, when given those arguments. This is how
fast f jiggles compared to g's jiggling, at the specific
point described by the arguments. (The specific point matters
because, for instance, the value of h might affect f's
jiggling, and h could give different values for different
arguments.)
gives, when given the values that
g and h give, when given those arguments. This is how
fast f jiggles compared to g's jiggling, at the specific
point described by the arguments. (The specific point matters
because, for instance, the value of h might affect f's
jiggling, and h could give different values for different
arguments.)
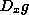 is a function. It takes the same
arguments as g does. Its the partial derivatives of g
with respect to its argument x. It is how fast g
jiggles with respect to jiggles in x.
is a function. It takes the same
arguments as g does. Its the partial derivatives of g
with respect to its argument x. It is how fast g
jiggles with respect to jiggles in x.
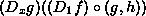 is a function. It takes the same arguments
as g and h do. Its values are the product of the values
given by
is a function. It takes the same arguments
as g and h do. Its values are the product of the values
given by 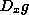 and
and 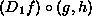 when these are given those same arguments. It is how fast f
jiggles given g's jiggling, times how fast g jiggles
given x's jiggles. All for some particular bunch of arguments.
when these are given those same arguments. It is how fast f
jiggles given g's jiggling, times how fast g jiggles
given x's jiggles. All for some particular bunch of arguments.
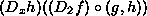 is a function. Its derivation and meaning
are similar. It is how fast f jiggles given h's
jiggling, times how fast h jiggles given x's jiggles.
All for some particular bunch of arguments.
is a function. Its derivation and meaning
are similar. It is how fast f jiggles given h's
jiggling, times how fast h jiggles given x's jiggles.
All for some particular bunch of arguments.
Finally,
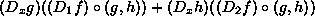 is a function. It takes the same arguments
as g and h do. Its values are the sum of the values
given by
is a function. It takes the same arguments
as g and h do. Its values are the sum of the values
given by 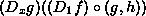 and
and 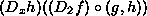 when
these are given those same arguments. It is the sum of f's
jiggling induced by g's jiggling, plus f's jiggling
induced by h's jiggling.
when
these are given those same arguments. It is the sum of f's
jiggling induced by g's jiggling, plus f's jiggling
induced by h's jiggling.
In summary, the right hand side of the equation, 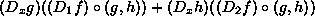 , tells how to calculate this jiggling in f,
caused via g and h, by the jiggles of their argument
x. It is the sum of two contributors. The first is how fast
f jiggles when g is jiggled by x, and the second
is how fast f jiggles when h is jiggled. The
Aha! neatness of this equation is that the contributions via
g and via h are independent of each other. One could
imagine this not being the case - there could have been some weird
interrelationship between the two contributions. The insight is that
the contribution of g's jiggling to f's jiggling is not
affected by h's jiggling, and visa versa. They are
independent, and thus can be computed separately and then simply added
together.
, tells how to calculate this jiggling in f,
caused via g and h, by the jiggles of their argument
x. It is the sum of two contributors. The first is how fast
f jiggles when g is jiggled by x, and the second
is how fast f jiggles when h is jiggled. The
Aha! neatness of this equation is that the contributions via
g and via h are independent of each other. One could
imagine this not being the case - there could have been some weird
interrelationship between the two contributions. The insight is that
the contribution of g's jiggling to f's jiggling is not
affected by h's jiggling, and visa versa. They are
independent, and thus can be computed separately and then simply added
together.
Now you can perhaps go back, look at the classical notation, and
see the meaning there. This ability to more or less understand the
classical notation once you know what you are looking for, are
what allow it to be used at all. The necessity, to you know
what you are looking for, is what makes the classical notation such a
bane for students, and trap for professional users.
[This section is basically just a placeholder.]
The functional version of the above equation can be
straightforwardly converted into a form which can be executed.
Rather loosely, in a dialect of Scheme:
(define (indirect-jiggling-function f g h x)
(+ (* ((partial x) g)
(((partial 1) f) g h))
(* ((partial x) h)
(((partial 2) f) g h))))
More credits:
The equation images where created using
Nikos Drakos's
LaTeX2HTML.
Comments encouraged. -
mcharity@lcs.mit.edu.
[Musings][Top]
Doables:
Add comment `This will become a non-issue given existence of developing
standards for electronic interchange of mathematics'.
History:
2001.Apr.20 Added link to SICM.
1999.Apr.06 Corrected a spelling error ("wierd") pointed out by a reader.
1996.Dec.05 A quick cleanup pass.
1996.Nov.23 Cleaned up a bit more.
1996.Nov.22 Cleaned up a bit.
1996.Nov.18 Created really crufty initial draft.
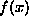
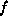
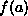 or
or 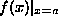
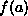
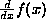
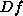
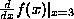
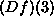
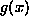
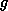
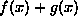
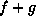
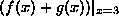
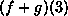
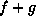 when it is evaluated at 3
(namely the sum of the values of f and g when both are evaluated at 3)
when it is evaluated at 3
(namely the sum of the values of f and g when both are evaluated at 3) 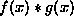
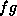
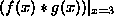
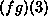
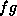 when it is evaluated at 3
(namely the product of the values of f and g when both are
evaluated at 3)
when it is evaluated at 3
(namely the product of the values of f and g when both are
evaluated at 3)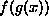
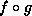
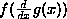
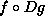
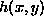
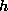
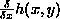
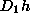
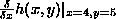
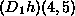
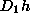 when evaluated at (4,5)
(namely, the partial derivative of h, in the neighborhood of (4,5),
with respect to its first argument)
when evaluated at (4,5)
(namely, the partial derivative of h, in the neighborhood of (4,5),
with respect to its first argument)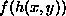

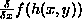
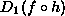
 with respect to its 1st argument.
with respect to its 1st argument.
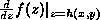
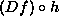
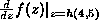
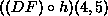
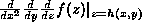
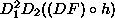
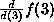 nonsense).
nonsense).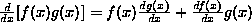 ,
, 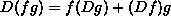 .
.
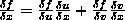
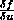 ,
, 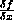 ,
, 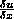 ):
):
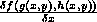
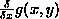
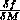 means just by looking at it? No. To disambiguate it one has to play
detective and examine the variables and the surrounding text.
means just by looking at it? No. To disambiguate it one has to play
detective and examine the variables and the surrounding text.
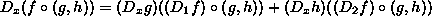
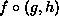 is a function. It takes the same
arguments as g and h take (thus g and h
must both be taking the same kind of arguments). f itself
takes two arguments, one from g and one from h.
The function gives the values f gives, when f is given
the values g and h give, when both given same
arguments.
Expressed differently: there are some arguments. g and
h independently chew on them. Their two results are given to
f, which then provides the final result.
is a function. It takes the same
arguments as g and h take (thus g and h
must both be taking the same kind of arguments). f itself
takes two arguments, one from g and one from h.
The function gives the values f gives, when f is given
the values g and h give, when both given same
arguments.
Expressed differently: there are some arguments. g and
h independently chew on them. Their two results are given to
f, which then provides the final result.
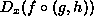 is a function. It is the derivative of
is a function. It is the derivative of
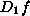 is a function. It takes the same
arguments as f does. Its the partial derivatives of f
with respect to its first argument. This is how fast f
jiggles, in general, compared to its first argument's jiggling.
is a function. It takes the same
arguments as f does. Its the partial derivatives of f
with respect to its first argument. This is how fast f
jiggles, in general, compared to its first argument's jiggling. 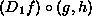 is a function. It takes the same
arguments as g and h do. Its values are the values the
function
is a function. It takes the same
arguments as g and h do. Its values are the values the
function 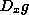 is a function. It takes the same
arguments as g does. Its the partial derivatives of g
with respect to its argument x. It is how fast g
jiggles with respect to jiggles in x.
is a function. It takes the same
arguments as g does. Its the partial derivatives of g
with respect to its argument x. It is how fast g
jiggles with respect to jiggles in x.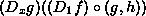 is a function. It takes the same arguments
as g and h do. Its values are the product of the values
given by
is a function. It takes the same arguments
as g and h do. Its values are the product of the values
given by 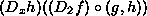 is a function. Its derivation and meaning
are similar. It is how fast f jiggles given h's
jiggling, times how fast h jiggles given x's jiggles.
All for some particular bunch of arguments.
is a function. Its derivation and meaning
are similar. It is how fast f jiggles given h's
jiggling, times how fast h jiggles given x's jiggles.
All for some particular bunch of arguments. 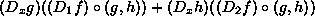 is a function. It takes the same arguments
as g and h do. Its values are the sum of the values
given by
is a function. It takes the same arguments
as g and h do. Its values are the sum of the values
given by